杂

1.一串数字转字符串

1
2
3
4
5
6
7
8
9
10
string s;
int a;
cin>>a;
stringstream aq;
aq<<a;
aq>>s;//s = aq.str();

cout<<s;
int sum=s.length() ;
cout<<sum;

2.求一句英文句子中每个单词有几个字母

string s;
int a, sum=0;
getline(cin, s);//输入一句，不会被空格阻断
stringstream ss;
ss.clear();
ss.str(s);
while(ss >> s)
{
    cout<<s.length() <<endl;
}

3.万能模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<bits/stdc++.h>//万能头
#pragma GCC optimize(2)
using namespace std;
typedef pair<int,int>PII; //pair
typedef unsigned long long ull;
typedef long long LL;
const int M=2010;
const int INF=0x3f3f3f3f;//最大值
const int mod=1e9+7;
const int N=2e5+10;
int dx[4]={0,1,0,-1};
int dy[4]={-1,0,1,0};
void solve()
{
        
}
int main()
{
		//只用cin>>,加速
        ios_base::sync_with_stdio(0);
        cin.tie(0);
        cout.tie(0);
        //文件操作
        freopen("test.in","r",stdin);
        int t;cin>>t;
        while(t--)solve();
        return 0;
}

4.最小公倍数

1
2
3
4
5
最小公倍数=a*b/最大公因数

二分要先大于目标值

并查集学习网址：https://blog.csdn.net/the_ZED/article/details/105126583?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164318091316780269847701%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=164318091316780269847701&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_ecpm_v1~rank_v31_ecpm-3-105126583.pc_search_result_cache&utm_term=%E5%B9%B6%E6%9F%A5%E9%9B%86&spm=1018.2226.3001.4187

5.四舍五入

1
2
round()//函数
(int)(a*1.0/b+0.5)

6.去重

1
2
int a[10];
int start=unique(a,a+10)-a;

7.位数

1
2
3
int num;
cin>>num;
cout<<setw(5)<<setfill('2')<<num<<endl;

8.lc sort（）排序定义

1
sort(words.begin(),words.end(),[&](string& a, string &b){}

9.else注意数值是否需要恢复初始化

10.n&(1<<i)是将左移i位的1与n进行按位与，即为保留n的第i位，其余位置零

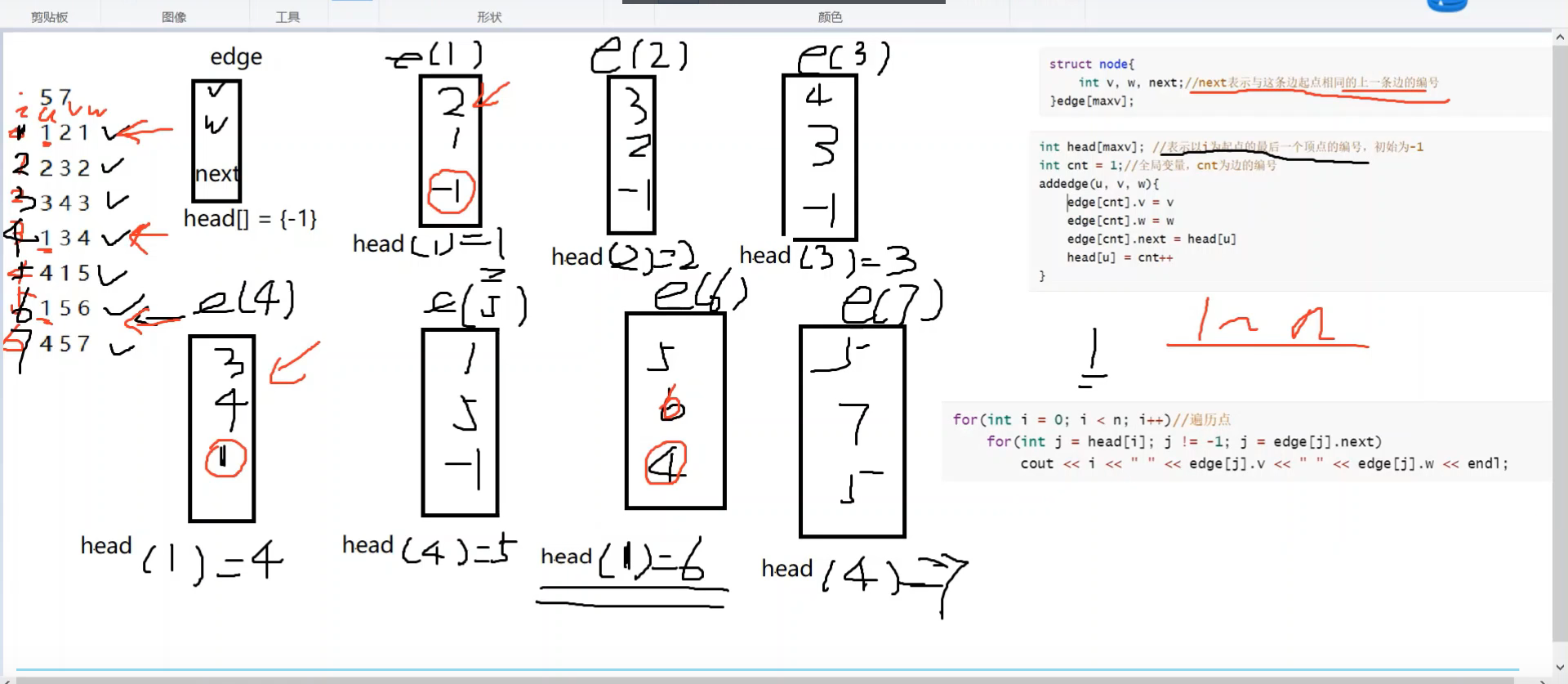
11.一维数组 邻接表 https://www.bilibili.com/video/BV14o4y1d7vv?spm_id_from=333.337.search-card.all.click

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6;
int h[maxn], ne[maxn], idx, e[maxn];
void add(int u, int v)
{
    e[idx] = v;
    ne[idx] = h[u];
    h[u] = idx++;
}
int main()
{
    freopen("a.in", "r", stdin);
    freopen("b.out", "w", stdout);
    memset(h, -1, sizeof h); //初始化邻接表
    int n, m, u, v, temp = 0;
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        cin >> u >> v;
        add(u, v);
        if (i == 1)
            temp = u;
    }
    for (int i = 0; i < n; i++)
    {
        for (int j = h[i]; j != -1; j = ne[j])
        {
            cout << i << " " << e[j] << endl;
            // 这是倒着输出，第一次输出的是，一个的最后位置之后往前递推
        }
    }
    system("pause");
    return 0;
}

12.小数位输出

1
cout<<fixed<<setprecision(6)<<res<<endl;

13.排列组合

https://zhuanlan.zhihu.com/p/41855459

14.第一个大于

1
2
cout << (lower_bound(a, a + 5, 1) - a) << endl;
    // 第一个大于等于1的元素是1，下标是0
1
2
cout << (upper_bound(a, a + 5, 2) - a) << endl;
    // 第一个大于2的元素是3，下标是1

二分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
while(r1-l1>0.00001)
            {
                dll mid=(r1+l1)/2;
                if(test(mid)*test(l1)<=0)
                {
                    r1=mid;
                }else
                {
                    l1=mid;
                }
            }
            printf("%.2lf ",l1);
//l1和r1没区别

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int main()
{
	int l;
	int r;
	while(l <= r)
	{
		int mid = (l + r )/ 2;  
		if(check())
		{
			ans = mid;  // 这里需要保证 check()函数是找最佳值的位置的。
						//  这个位置已经满足一个位置了，再往mid - 1位置找看是否还有更佳位置
			l = mid+ 1;
		}
		else
		{
			r = mid-1;
		}
} 
	//答案是ans 或者返回l
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<bits/stdc++.h>
using namespace std;
int main()
{
    freopen("b.out","w",stdout);
	int a[10];
	for(int i=0;i<10;i++)
	{
		a[i]=10;
	}
	cout<<"找最靠前的值："<<endl;
	int l=0,r=9;
	while(l<r)
	{
		int mid=l+r>>1;
		if(a[mid]>=10)r=mid;
		else l=mid+1;
	}
	cout<<l<<endl;
	cout<<"找最靠后的："<<endl;
	l=0;r=9;
	while(l<r)
	{
		int mid=l+r+1>>1;
		if(a[mid]<=10)l=mid;
		else r=mid-1;
	}
	cout<<l<<endl;

	return 0;
}

最大公约数和最小公倍数

1
2
3
int lcm(int a, int b) { return a * b / gcd(a, b); }    最小公倍数

int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); } 最大公约数

floyd算法

2021蓝桥javaB路径

https://blog.csdn.net/qq_43196686/article/details/115836954

（耗时极大）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
using namespace std;
typedef long long ll;
int min(int a, int b) { return a < b ? a : b; }
int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }
int lcm(int a, int b) { return a * b / gcd(a, b); }

const int N = 2021;
int num[N + 1][N + 1];
int main()
{

    for (int i = 1; i < N; i++)
    {
        for (int j = i+1; j <= min(i+21,N); j++)
        {
            num[i][j] = lcm(i, j);
            num[j][i] = lcm(i, j);
        }
    }
    for (int k = 1; k <= N; k++)
    {
        for (int i = 1; i <= N; i++)
        {
            if (num[i][k] == 0)
                continue;
            for (int j = 1; j <= N; j++)
            {
                if (num[k][j] == 0)
                    continue;
                else if (num[i][j] == 0 || (num[i][j] > num[i][k] + num[k][j]))
                    num[i][j] = num[i][k] + num[k][j];
            }
        }
    }
    cout << num[1][2021] << endl;
    system("pause");

    return 0;
}

Dijkstra求最短路

https://www.acwing.com/problem/content/description/851/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int min(int a, int b) { return a < b ? a : b; }
int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }
int lcm(int a, int b) { return a * b / gcd(a, b); }
int edges[550][550];
int dist[550];    //到出发点的距离
int visited[550]; //所有点是否被丢弃
int n, m;
int dijkstra(int n1, int m1)
{
    for (int i = 0; i < n1; i++)
    {
        int index = -1;
        dist[1] = 0;
        for (int j = 1; j <= n1; j++)
        {
            if (!visited[j] && (index == -1 || dist[j] < dist[index]))
            {
                index = j;
            }
        }
        visited[index] = 1;
        for (int j = 1; j <= n1; j++)
        {
            if (dist[index] + edges[index][j] < dist[j])
            {
                dist[j] = dist[index] + edges[index][j];
            }
        }
    }
    if (dist[n1] == 0x3f3f3f3f)
    {
        return -1;
    }
    else
    {
        return dist[n1];
    }
}
int main()
{
    memset(edges, 0x3f, sizeof(edges));
    cin >> n >> m;
    int a, b, c;
    for (int i = 0; i < m; i++)
    {
        cin >> a >> b >> c;
        edges[a][b] = edges[a][b] > c ? c : edges[a][b];
    }
    memset(dist, 0x3f, sizeof(dist));
    memset(visited, 0, sizeof(visited));
    cout << dijkstra(n, m) << endl;
    return 0;
}

快速幂

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<bits/stdc++.h>
using namespace std;
int test(int a,int b,int c)
{
    int res=1;
    while(b)
    {
        if(b&1)res=(res*a)%c;
        a=(a*a)%c;
        b>>=1;
    }
    return res;
}
int main()
{
    cout<<test(2,5,10)<<endl;
    system("pause");
    return 0;
}

矩陣快速冪

单个横行和竖行的矩阵值为O，相当于乘法里的1；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1000000009;
struct st
{
	ll aa[2][2];
};
st mul(st x,st y)
{
	st c;
	memset(c.aa,0,sizeof(c.aa));
	for(int i=0;i<2;i++)
	{
		for(int j=0;j<2;j++)
		{
			for(int k=0;k<2;k++)
			{
				c.aa[i][j]=(c.aa[i][j]+x.aa[i][k]*y.aa[k][j])%mod;;
			}
		}
	}
	return c;
}

ll test(ll a)
{
	st base,base1;
	memset(base.aa,0,sizeof(base.aa));
	memset(base1.aa,0,sizeof(base1.aa));
	for(int i=0;i<2;i++)
	{
		base.aa[i][i]=1;
	}
	base1.aa[0][0]=base1.aa[0][1]=base1.aa[1][0]=1;
	while(a)
	{
		if(a&1)base=mul(base,base1);
		base1=mul(base1,base1);
		a>>=1;
	}
	return base.aa[0][1];
}
int main()
{
	ll num;
	cin>>num;
	cout<<test(num)<<endl;
	return 0;
}

并查集

https://vjudge.net/contest/479411#problem/F

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include<bits/stdc++.h>
4using namespace std;
const int maxn=10e6+1;
int a[maxn];
int b[maxn];
void init(int num)
{
    for(int i=1;i<=num;i++)
    {
        a[i]=i;
    }
}
int find(int key)
{
    if(a[key]==key)return key;
    else return a[key]=find(a[key]);
}
void unit(int x1,int y1)
{
    int xx1=find(x1);
    int yy1=find(y1);
    if(xx1!=yy1)
    {
        a[xx1]=yy1;
    }
}
int main()
{
  
    int n,m;
    cin>>n>>m;
    init(n);
    int a1,b1,c1;
    for(int i=0;i<m;i++)
    {
        cin>>a1>>b1>>c1;
        if(a1==1)
        {
            unit(b1,c1);
        }
        else if(a1==2)
        {
            if(find(b1)!=find(c1))
            {
                cout<<"NO"<<endl;
            }else{
                cout<<"YES"<<endl;
            }
        }
    }
    return 0;
}

拓扑排序

https://vjudge.net/contest/479411#problem/J

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <bits/stdc++.h>

using namespace std;
const int maxn = 101;
int lin[maxn][maxn];
int ss[maxn];
int value[maxn];
int a, b, m, n;
queue<int> qq;
void TP()
{
    for (int i = 1; i <= a; i++)
    {
        for (int j = 1; j <= a; j++)
        {
            if (lin[i][j] == 1)
            {
                ss[j]++;
            }
        }
    }
    for (int i = 1; i <= a; i++)
    {
        int k = 1;
        while (ss[k] != 0)
            k++;
        value[i] = k;
        ss[k] = -1;
        for (int j = 1; j <= a; j++)
        {
            if (lin[k][j] == 1)
                ss[j]--;
        }
    }
}
int main()
{
    while (scanf("%d%d", &a, &b) != EOF)
    {
        if (!(a + b))
            break;
        memset(ss, 0, sizeof(ss));
        memset(lin, 0, sizeof(lin));
        memset(value, 0, sizeof(value));
        for (int i = 0; i < b; i++)
        {
            cin >> m >> n;
            if (i != b)
                lin[m][n] = 1;
        }
        TP();
        for (int i = 1; i <= a; i++)
        {
            cout << value[i] << " ";
        }
        cout << endl;
    }

    return 0;
}

bfs简单例题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<iostream>
#include<queue>

using namespace std;
const int maxn= 100001;
bool ha[maxn];
int pl[maxn];
queue<int> qq;
int bfs(int a1,int b1)
{
    qq.push(a1);
    ha[a1]=true;
    int next=0;
    while(qq.size())
    {
        int temp=qq.front();
        qq.pop();
        for(int i=0;i<3;i++)
        {
            if(i==0)next=temp-1;
            else if(i==1)next=temp+1;
            else next=temp*2;
            if(next<0||next>=maxn)continue;
            if(!ha[next])
            {
                qq.push(next);
                ha[next]=true;
                pl[next]=pl[temp]+1;
            }
            if(next==b1)return pl[b1];
        }
    }
}
int main()
{

    int a,b;
    cin>>a>>b;
    if(a>=b)
    cout<<a-b<<endl;
    else
    cout<<bfs(a,b)<<endl;
    return 0;
}

bfs简单例题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
#include<iostream>

#include<cstdio>

#include<cstring>

#include<algorithm>

#include<queue>

#include<string>

#include<math.h> 

using namespace std;

const int maxn=20;

int n,m;

char a[maxn][maxn];

int vis[maxn][maxn];

int ans=99999;

int dir[4][2]={{0,-1},{1,0},{0,1},{-1,0}};

int sx,sy,fx,fy;

struct node {

  int x,y;

  int step;

  node(int xx,int yy,int ss):x(xx),y(yy),step(ss){ }//可以使下面可以创建一个结点直接使用

  //比如说node(1,1,1)就可以直接使用,而不加这个的话会报错

};

queue<node> q;

bool pd(int x,int y)//判断可以通过的条件

{

  if(x>=1&&x<=n&&y>=1&&y<=m&&vis[x][y]==0&&a[x][y]!='#')

  //没有越界,且没被遍历,且不是墙

  {

    return true;

  }

  else

  return false;

}

void bfs(int x,int y)

{

  vis[x][y]=1;

  q.push(node(x,y,0));

  while(!q.empty())

  {

  node now=q.front();

  q.pop();

  for(int i=0;i<4;i++)

  {

    if(now.x+1>n||now.y+1>m||now.x-1<1||now.y-1<1)//判断下一步是否可以走出去

      ans=min(ans,now.step);//最短路的判断

  }

  for(int i=0;i<4;i++)

  {

    int nx=now.x+dir[i][0];

    int ny=now.y+dir[i][1];

    if(pd(nx,ny))

    {

      vis[nx][ny]=1;

      q.push(node(nx,ny,now.step+1));

    }

  }

  }

}

int main()

{

  memset(vis,0,sizeof(vis));

  cin>>n>>m;

  for(int i=1;i<=n;i++)

  {

  for(int j=1;j<=m;j++)

  {

    cin>>a[i][j];

    if(a[i][j]=='@')

    {

      sx=i;

      sy=j;

    }

  }

  }

  bfs(sx,sy);

  if(ans==99999)

  {

  cout<<-1;

  }

  else

  {

  cout<<ans<<endl;

  } 

}

dfs简单例题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <iostream>
#include <cstdio>
using namespace std;

int R, C;
int map[105][105];
int mark[105][105] = {0};

int dfs(int i, int j)
{
    int k;
    if (mark[i][j])
        return mark[i][j];//
    if (i != 0 && map[i - 1][j] < map[i][j])
    {
        k = dfs(i - 1, j) + 1;
        if (k > mark[i][j])
            mark[i][j] = k;
    }
    if (i != R - 1 && map[i + 1][j] < map[i][j])
    {
        k = dfs(i + 1, j) + 1;
        if (k > mark[i][j])
            mark[i][j] = k;
    }
    if (j != 0 && map[i][j - 1] < map[i][j])
    {
        k = dfs(i, j - 1) + 1;
        if (k > mark[i][j])
            mark[i][j] = k;
    }
    if (j != C - 1 && map[i][j + 1] < map[i][j])
    {
        k = dfs(i, j + 1) + 1;
        if (k > mark[i][j])
            mark[i][j] = k;
    }
    return mark[i][j];
}

int main()
{
    int i, j, k, sum = 0;
    scanf("%d%d", &R, &C);
    for (i = 0; i < R; i++)
    {
        for (j = 0; j < C; j++)
        {
            scanf("%d", &map[i][j]);
        }
    }
    for (i = 0; i < R; i++)
    {
        for (j = 0; j < C; j++)
        {
            k = dfs(i, j);
            if (k > sum)
                sum = k;
        }
    }
    cout << sum + 1 << endl;
    return 0;
}

字典树–前缀树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<bits/stdc++.h>
using namespace std;
const int maxn=10e5;
static int trie[maxn][26];
static int count1[maxn];
static int index=0;
void insert(string s)//这里是插入数据
{
	int p=0;
	for(int i=0;i<s.length();i++)
	{
		int u=s[i]-'a';
		if(trie[p][u]==0)trie[p][u]=++index;
		p=trie[p][u];
	}
	count1[p]++;
}
bool search(string s)//这里是完全搜索数据
{
	int p=0;
	for(int i=0;i<s.length();i++)
	{
		int u=s[i]-'a';
		if(trie[p][u]==0)return false;
		p=trie[p][u];
	}
	return count1[p]!=0;
}
bool searchstart(string s)//这里是只搜索前缀是否有共同的
{
	int p=0;
	for(int i=0;i<s.length();i++)
	{
		int u=s[i]-'a';
		if(trie[p][u]==0)return false;
		p=trie[p][u];
	}
	return true;
}
int main()
{	
	insert("aaa");
	cout<<search("aa")<<" "<<search("aaa")<<" "<<search("aaaa")<<endl;
	cout<<searchstart("a")<<" "<<searchstart("aaa")<<" "<<searchstart("aaaa")<<endl;
	system("pause");
	return 0;
}

dfs—1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
问题 C: 【递归入门】组合+判断素数
时间限制: 1 Sec  内存限制: 128 MB
提交: 205  解决: 77
[提交][状态][讨论版][命题人:外部导入]

题目描述
已知 n 个整数b1,b2,…,bn
以及一个整数 k（k＜n）。
从 n 个整数中任选 k 个整数相加，可分别得到一系列的和。
例如当 n=4，k＝3，4 个整数分别为 3，7，12，19 时，可得全部的组合与它们的和为：
　　　　3＋7＋12=22　　3＋7＋19＝29　　7＋12＋19＝38　　3＋12＋19＝34。
现在，要求你计算出和为素数共有多少种。
例如上例，只有一种的和为素数：3＋7＋19＝29。
输入
第一行两个整数：n , k （1<=n<=20，k＜n） 
第二行n个整数：x1,x2，…,xn （1<=xi<=5000000） 
输出
一个整数（满足条件的方案数）。 
样例输入
4 3
3 7 12 19
样例输出
1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include<bits/stdc++.h>
using namespace std;
const int maxn=25;
int a[maxn];
int p[maxn];
bool vis[maxn];
int n,k,ans=0,sum;
bool test(int num)
{
    if(num<=1)
    {
        return false;
    }
    for(int i=2;i*i<=num;i++)
    {
        if(num%i==0)
        return false;
    }
    return true;
}
void dfs(int index)
{
    if(index==k+1)
    {
        if(test(sum))
        ans++;
        for(int i=1;i<=index-1;i++)
        {
            cout<<p[i]<<" ";
        }
        cout<<sum;
        cout<<endl;
        return ;
    }
    for(int i=1;i<=n;i++)
    {
        if(vis[i]==false&&i>p[index-1])
        {
            p[index]=i;
            vis[i]=true;
            sum+=a[i];
            dfs(index+1);
            vis[i]=false;
            sum-=a[i];
        }
    }
}
int main()
{
    cin>>n>>k;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        p[i]=i;
    }
    dfs(1);
    cout<<ans<<endl;
    system("pause"); 
    return 0;
}

spfa1–环里有负值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5 + 10;
int e[maxn],h[maxn],w[maxn],ne[maxn],idx;
int dist[maxn],st[maxn];
int m,n;
void add(int a,int b,int c)
{
    e[idx]=b;
    w[idx]=c;
    ne[idx]=h[a];
    h[a]=idx++;
}
int spfa()
{
    memset(dist,0x3f,sizeof(dist));
    dist[1]=0;
    queue<int>qq;
    qq.push(1);
    st[1]=1;
    while(qq.size())
    {
        auto t=qq.front();
        qq.pop();
        st[t]=0;
        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(dist[j]>dist[t]+w[i])
            {
                dist[j]=dist[t]+w[i];
                if(!st[j])
                {
                    qq.push(j);
                    st[j]=1;
                }
            }
        }

    }
    if(dist[n]==0x3f3f3f3f)
    {
        return -0x3f3f3f3f;
    }
    return dist[n];
    

}
int main()
{
    memset(h,-1,sizeof(h));
    cin>>n>>m;
    for(int i=0;i<m;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c);
    }
    if(spfa()==-0x3f3f3f3f){
        cout<<"impossible"<<endl;
    }else{
        cout<<dist[n]<<endl;
    }
    return 0;
}

spfa–判断负环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5 + 10;
int e[maxn],h[maxn],w[maxn],ne[maxn],idx;
int dist[maxn],st[maxn],cnt[maxn];
int m,n;
void add(int a,int b,int c)
{
    e[idx]=b;
    w[idx]=c;
    ne[idx]=h[a];
    h[a]=idx++;
}
bool spfa()
{
    queue<int>qq;
    for(int i=1;i<=n;i++)
    {
    qq.push(i);
    st[1]=1;
    }
    
    while(qq.size())
    {
        auto t=qq.front();
        qq.pop();
        st[t]=0;
        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(dist[j]>dist[t]+w[i])
            {
                dist[j]=dist[t]+w[i];
                cnt[j]=cnt[t]+1;
                if(cnt[j]>=n)return true;
                if(!st[j])
                {
                    qq.push(j);
                    st[j]=1;
                }
            }
        }

    }
    return false;
    

}
int main()
{
    memset(h,-1,sizeof(h));
    cin>>n>>m;
    for(int i=0;i<m;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c);
    }
    if(spfa()){
        cout<<"Yes"<<endl;
    }else{
        cout<<"No"<<endl;
    }
    system("pause");
    return 0;
}

求逆元

1.快速幂相对第二种慢一些

image-20220909135404749

题目链接—https://www.luogu.com.cn/problem/P3811

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll test(ll x,ll y,ll z)
{
    ll sum=1;
    ll ans=x%z;
    while(y)
    {
        if(y&1)
        {
            sum=(sum*ans)%z;
        }
        ans=(ans*ans)%z;
        y>>=1;
    }
    return sum;
}
int main()
{
    freopen("a.in", "r", stdin);
    freopen("b.out", "w", stdout);
    ll n,mod;
    cin>>n>>mod;
    for(ll i=1;i<=n;i++)
    {
        cout<<test(i,mod-2,mod)<<endl;
    }
    

    return 0;
}

2.线性时间复杂度

这里主要是最好用节省时间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<cstdio>
using namespace std;
long long inv[3000010];
int main()
{
    long long  n,mod;
    scanf("%lld%lld",&n,&mod);
    printf("1\n");
    inv[1]=1;
    for(int i=2;i<=n;i++)
    {
        inv[i]=mod-(mod/i)*inv[mod%i]%mod;
        printf("%lld\n",inv[i]);
    }
    return 0;
}

线段树

1.最简单的 题目在下面

https://img-blog.csdnimg.cn/2020021217471941.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NTY5Nzc3NA==,size_16,color_FFFFFF,t_70

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6;
ll arr[maxn];
struct st
{
    ll l;
    ll r;
    ll sum;
} tree[maxn];
void build(int i, int l, int r)
{
    tree[i].l = l;
    tree[i].r = r;
    if (l == r)
    {
        tree[i].sum = arr[l];
        return;
    }
    ll mid = (l + r) >> 1;
    build(i * 2, l, mid);
    build(i * 2 + 1, mid + 1, r);
    tree[i].sum = tree[i * 2].sum * tree[i * 2 + 1].sum;
}
ll search(ll i, ll l, ll r)
{
    if (tree[i].l >= l && tree[i].r <= r)
        return tree[i].sum;
    ll res = 1;
    if (tree[i * 2].r >= l)
    {
        res = (res * search(i * 2, l, r));
    }
    if (tree[i * 2 + 1].l <= r)
    {
        res = (res * search(i * 2 + 1, l, r));
    }
    return res;
}
int main()
{
   
    ll n, k;
    cin >> n >> k;
    for (int i = 1; i <= n; i++)
    {
        cin >> arr[i];
    }
    build(1, 1, n);
    ll ans = 0;
    for (int i = 1; i <= n - k; i++)
    {
        ans = max(ans, search(1, i, i + k - 1));
    }
    cout << ans << endl;
    return 0;
}

2.简单的模板 随意加和查询

https://www.luogu.com.cn/problem/P3372

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
#include <bits/stdc++.h>
using namespace std;
const int maxn = 10e6;
typedef long long ll;
ll arr[maxn];

struct st
{
    ll l, r, sum, lz;
} tree[maxn];

void build(ll i, ll l, ll r, ll *arr)
{
    tree[i].l = l;
    tree[i].r = r;
    tree[i].lz = 0;
    if (l == r)
    {
        tree[i].sum = arr[l];
        return ;
    }
    ll mid = (l + r) >> 1;
    build(i * 2, l, mid, arr);
    build(i * 2 + 1, mid + 1, r, arr);
    tree[i].sum = tree[i * 2].sum + tree[i * 2 + 1].sum;
    return;
}
<!-- 主要作用是不让往下遍历（标记），直接存这里就好，之后（搜索查找的时候再传下去）或者再次添加的时候传下去，保证结果正确 -->
void push_down(ll i)
{
    if (tree[i].lz != 0)
    {
        tree[i * 2].lz += tree[i].lz;
        tree[i * 2 + 1].lz += tree[i].lz;
        int mid = (tree[i].l + tree[i].r) / 2;
        tree[i * 2].sum += tree[i].lz * (mid - tree[i * 2].l + 1);
        tree[i * 2 + 1].sum += tree[i].lz * (tree[i * 2+1].r - mid);
        tree[i].lz = 0;
    }
    return;
}

void add(ll i, ll l, ll r, ll k)
{
    if (tree[i].l >= l && tree[i].r <= r)
    {
        tree[i].sum += k * (tree[i].r - tree[i].l + 1);
        tree[i].lz += k;
        return;
    }
    push_down(i);
    if (tree[i * 2].r >= l)
    {
        add(i * 2, l, r, k);
    }
    if (tree[i * 2 + 1].l <= r)
    {
        add(i * 2 + 1, l, r, k);
    }
    tree[i].sum = tree[i * 2].sum + tree[i * 2 + 1].sum;
    return;
}

ll searchs(ll i, ll l, ll r)
{
    if (tree[i].l >= l && tree[i].r <= r)
    {
        return tree[i].sum;
    }
    push_down(i);
    ll num = 0;
    if (tree[i * 2].r >= l)
    {
        num += searchs(i * 2, l, r);
    }
    if (tree[i * 2 + 1].l <= r)
    {
        num += searchs(i * 2 + 1, l, r);
    }
    return num;
}

int main()
{
    freopen("a.in", "r", stdin);
    freopen("b.out", "w", stdout);
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    ll n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        cin >> arr[i];
    }
    build(1, 1, n, arr);
    for (int i = 1; i <= m; i++)
    {
        int temp;
        cin >> temp;
        if (temp == 1)
        {
            ll a, b, c;
            cin >> a >> b >> c;
            add(1, a, b, c);
        }
        else
        {
            ll a, b;
            cin >> a >> b;
            cout << searchs(1, a, b)<<endl;
        }
    }

    return 0;
}

最小生成树

https://blog.csdn.net/qq_43619271/article/details/109091314?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522165121095416782184637180%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=165121095416782184637180&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~blog~top_positive~default-1-109091314.nonecase&utm_term=%E6%9C%80%E5%B0%8F%E7%94%9F%E6%88%90%E6%A0%91&spm=1018.2226.3001.4450

prim

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <bits/stdc++.h>
using namespace std;
const int maxn = 505;
int INF = 0x3f3f3f3f;
int edge[maxn][maxn];
int dist[maxn], vis[maxn];
int n, m, u, v, w;
long long sum = 0;
long long prime(int pos)
{
    dist[pos] = 0;
    for (int i = 1; i <= n; i++)
    {
        int cur = -1;
        for (int j = 1; j <= n; j++)
        {
            if (!vis[j] && (cur == -1 || dist[j] < dist[cur]))
            {
                cur = j;
            }
        }
        if (dist[cur] >= INF)
            return INF;
        sum += dist[cur];
        vis[cur] = 1;
        for (int k = 1; k <= n; k++)
        {
            if (!vis[k])
                dist[k] = min(dist[k], edge[cur][k]);
        }
    }
    return sum;
}

int main()
{
    freopen("a.in", "r", stdin);
    freopen("b.out", "w", stdout);
    cin >> n >> m;
    memset(dist, 0x3f, sizeof(dist));
    memset(edge, 0x3f, sizeof(edge));
    for (int i = 1; i <= m; i++)
    {
        cin >> u >> v >> w;
        edge[u][v] = min(edge[u][v],w);
        edge[v][u] = min(edge[v][u],w);
    }
    long long value = prime(1);
    if (value >= INF)
    {
        cout << "impossible" << endl;
    }
    else
    {
        cout << value << endl;
    }
    return 0;
}

Kruskal算法求最小生成树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <bits/stdc++.h>
using namespace std;
const int maxn = 10e6;
struct st
{
    int x;
    int y;
    int z;
} edge[maxn];
int  fa[maxn];
long long sum=0;
int find1(int key)
{
    if (fa[key] == key)
    {
        return key;
    }
    else
        return fa[key] = find1(fa[key]);
}
bool cmp(st s1, st s2)
{
    return s1.z < s2.z;
}
int main()
{
    long long n, m;
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        cin >> edge[i].x >> edge[i].y >> edge[i].z;
    }
    for (int i = 0; i <= n; i++)
    {
        fa[i] = i;
    }
    sort(edge+1, edge + m+1, cmp);
    for (int i = 1; i <= m; i++)
    {
        int x = find1(edge[i].x);
        int y = find1(edge[i].y);
        if (x == y)
        {
            continue;
        }
        fa[x] = y;
        sum += edge[i].z;
    }
    int ans = 0;
    for (int i = 1; i <= n; i++)
    {
        if (i == fa[i])
        {
            ans++;
        }
    }
    if (ans > 1)
        cout << "impossible" << endl;
    else
        cout << sum;
    return 0;
}

二分图匹配

染色法判定二分图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6;
int h[N], e[N], ne[N], idx;
int color[N];
void add(int u, int v)
{
    e[idx] = v;
    ne[idx] = h[u];
    h[u] = idx++;
}
bool dfs(int i, int k)
{
    color[i] = k;
    for (int j = h[i]; j != -1; j = ne[j])
    {
        int b = e[j];
        if (!color[b])
        {
            if (!dfs(b, 3 - k))
                return false;
        }
        else if (color[b] && color[b] != 3 - k)
        {
            return false;
        }
    }
    return true;
}
int main()
{
    freopen("a.in", "r", stdin);
    freopen("b.out", "w", stdout);
    memset(h, -1, sizeof(h));
    int n, m;
    cin >> n >> m;
    int u, v;
    for (int i = 1; i <= m; i++)
    {
        cin >> u >> v;
        add(u, v);
        add(v, u);
    }
    for (int i = 0; i < n; i++)
    {
        if (!color[i])
        {
            if (!dfs(i, 1))
            {
                cout << "NO" << endl;
                return 0;
            }
        }
    }
    cout << "YES" << endl;
    return 0;
}

辛普森积分

https://blog.csdn.net/weixin_30444105/article/details/95306900?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522165132001016782390558168%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=165132001016782390558168&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2allsobaiduend~default-1-95306900.142^v9^pc_search_result_control_group,157^v4^control&utm_term=辛普森积分&spm=1018.2226.3001.4187

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <bits/stdc++.h>

using namespace std;

const double esp = 1e7;

typedef double db;

double a, b, c, d, L, R;

db f(db x)

{

  return (c * x + d) / (a * x + b);

}

db sim(db l, db r)

{

  return (f(l)+f(r)+4*f((l+r)/2))*(r-l)/6;

}

double asr(db L, db R,db esp ,db val)

{

  db mid=(L+R)/2;

  db lval=sim(L,mid);

  db rval=sim(mid,R);

  if(fabs(lval+rval-val)<=15*esp){return lval+rval+(lval+rval-val)/15;}

  return asr(L,mid,esp/2,lval)+asr(mid,R,esp/2,rval);

 

 

}

double asme(db L, db R, db esp)

{

  return asr(L, R, esp, sim(L, R));

}

int main()

{

 

  cin >> a >> b >> c >> d >> L >> R;

  cout <<fixed<<setprecision(6)<< asme(L, R, esp);

 

  return 0;

}

计算几何

*面积公式*

double area(BWE A,BWE B,BWE C)

{

//用于计算三角形面积的函数(直接套用题目中的公式)

​ return abs(A.x*(B.y-C.y)+B.x*(C.y-A.y)+C.x*(A.y-B.y))/2;

}

求两点之间的整数点个数

gcd(abs(a1-a2), abs(b1-b2));

皮克定理

其中a表示多边形内部的点数（就是题目中要求的答案)，b表示多边形恰好落在边界上的点数，s表示多边形的面积。 易知，a=S-b/2+1

旋转点

我们可以这样认为：对于任意点A(x,y)，A非原点，绕原点旋转θ角后点的坐标为： (xcosθ- y * sinθ, ycosθ + x * sinθ)、 如果不绕原点的话可以直接加减(xx,yy); (xcosθ- y * sinθ+xx, ycosθ + x * sinθ+yy)、 绕其他(x2,y2)点旋转 ((x-x2)*cosθ- (y-y2) * sinθ+x2, (y-y2)*cosθ + (x-x2) * sinθ+y2)

求凸包模板题

https://www.luogu.com.cn/problem/P2742

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;

int n, num = 1;

struct ben

{

    double x, y;

} p[100005], s[100005];

double check(ben a1, ben a2, ben b1, ben b2) //检查叉积是否大于0，如果是a就逆时针转到b

{

    return (a2.x - a1.x) * (b2.y - b1.y) - (b2.x - b1.x) * (a2.y - a1.y);
}

double d(ben p1, ben p2) //两点间距离。。。

{

    return sqrt((p2.y - p1.y) * (p2.y - p1.y) + (p2.x - p1.x) * (p2.x - p1.x));
}

bool cmp(ben lhs, ben rhs)
{

    if (check(p[1], lhs, p[1], rhs) < 0)
        return false;

    if (check(p[1], lhs, p[1], rhs) > 0)
        return true;

    return d(p[1], lhs) < d(p[1], rhs);
}

void add(double ll, double ff)

{

    double mid;

    p[num].x = ll, p[num].y = ff;

    if (p[num].y < p[1].y || (p[num].y == p[1].y && p[num].x < p[1].x))
    {

        swap(p[num], p[1]);
    }

    num++;

    return;
}

int main()

{

    // freopen("a.in","r",stdin);

    //  freopen("b.out","w",stdout);

    scanf("%d", &n);

    double mid, ll, ff;

    for (int i = 1; i <= n; i++)

    {

        scanf("%lf%lf", &ll, &ff);

        add(ll, ff);
    }

    sort(p + 2, p + 1 + n, cmp); //系统快排

    s[1] = p[1]; //最低点一定在凸包里

    int cnt = 1;

    for (int i = 2; i <= num - 1; i++)

    {

        while (cnt > 1 && check(s[cnt - 1], s[cnt], s[cnt], p[i]) < 0) //判断前面的会不会被踢走，如果被踢走那么出栈

            cnt--;

        cnt++;

        s[cnt] = p[i];
    }

    s[cnt + 1] = p[1]; //最后一个点回到凸包起点

    double ans = 0;

    for (int i = 1; i <= cnt; i++)

        ans += d(s[i], s[i + 1]); //然后s里存好了凸包序列，只需要把两两距离累加就行

    printf("%.2lf\n", ans);

    return 0;
}

求凸包 难一点

https://www.luogu.com.cn/problem/P3829

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
#include <iostream>

#include <algorithm>

#include <cstdio>

#include <cmath>

using namespace std;

#define eps 1e-12

int n, num = 1;

double a, b, r;

struct ben

{

  double x, y;

} p[1000005], s[1000005];

double check(ben a1, ben a2, ben b1, ben b2) //检查叉积是否大于0(小于180度)，等于零(平行)，如果是a就逆时针转到b

{

  return (a2.x - a1.x) * (b2.y - b1.y) - (b2.x - b1.x) * (a2.y - a1.y);

}

double d(ben p1, ben p2) //两点间距离。。。

{

  return sqrt((p2.y - p1.y) * (p2.y - p1.y) + (p2.x - p1.x) * (p2.x - p1.x));

}

bool cmp (ben lhs, ben rhs) {

  if (check (p[1], lhs, p[1], rhs) < 0) return false;

  if (check (p[1], lhs, p[1], rhs) > 0) return true;

  return d (p[1], lhs) < d (p[1], rhs);

}

void add(double ll, double ff)

{

  double mid;

  p[num].x = ll, p[num].y = ff;

  if (p[num].y < p[1].y || (p[num].y == p[1].y && p[num].x < p[1].x)) {

     swap (p[num], p[1]);

   }

  num++;

  return;

}

int main()

{

  freopen("a.in", "r", stdin);

  freopen("b.out", "w", stdout);

  scanf("%d%lf%lf%lf", &n, &b, &a, &r);

  a = a / 2.0;

  b = b / 2.0;

  double mid, xx, yx, th;

  for (int i = 1; i <= n; i++)

  {

 

   scanf("%lf%lf%lf", &xx, &yx, &th);

   xx += eps;

   yx += eps;

   th += eps;

   double s1 = sin(th);

   double c1 = cos(th);

   add((a - r) * c1 - (b - r) * s1 + xx, (b - r) * c1 + (a - r) * s1 + yx);

   // cout<<(a-r)*c1-(b-r)*s1+xx<<" " <<(b-r)*c1+(a-r)*s1+yx<<endl;

   add(-(a - r) * c1 - (b - r) * s1 + xx, (b - r) * c1 - (a - r) * s1 + yx);

   // cout<<-(a-r)*c1-(b-r)*s1+xx<<" "<<(b-r)*c1-(a-r)*s1+yx<<endl;

   add((a - r) * c1 + (b - r) * s1 + xx, -(b - r) * c1 + (a - r) * s1 + yx);

   // cout<<(a-r)*c1+(b-r)*s1+xx<<" "<< -(b-r)*c1+(a-r)*s1+yx<<endl;

   add(-(a - r) * c1 + (b - r) * s1 + xx, -(b - r) * c1 - (a - r) * s1 + yx);

   // cout<<-(a-r)*c1+(b-r)*s1+xx<<" "<<-(b-r)*c1-(a-r)*s1+yx<<endl;

  }

  // cout<<num<<endl;

  sort(p + 2, p + num, cmp); //系统快排

  s[1] = p[1];        //最低点一定在凸包里

  int cnt = 1;

  for (int i = 2; i <= num - 1; i++)

  {

   while (cnt > 1 && check(s[cnt - 1], s[cnt], s[cnt], p[i]) <= 0) //判断前面的会不会被踢走，如果被踢走那么出栈

     cnt--;

   cnt++;

   s[cnt] = p[i];

  }

  s[cnt + 1] = p[1]; //最后一个点回到凸包起点

  double ans = 0;

  for (int i = 1; i <= cnt; i++)

   ans += d(s[i], s[i + 1]); //然后s里存好了凸包序列，只需要把两两距离累加就行

  printf("%.2lf\n", ans + 3.141592653589793 * 2 * r);

  return 0;

}

旋转卡壳

https://www.luogu.com.cn/problem/P1452

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
#include <bits/stdc++.h>

using namespace std;

int n, num = 1;

int v = 2;

double ans = 0;

struct ben

{

    double x, y;

} p[100005], s[100005];

double check(ben u1, ben u2, ben v1, ben v2)
{

    return (u2.x - u1.x) * (v2.y - v1.y) - (u2.y - u1.y) * (v2.x - v1.x);
}

double d(ben p1, ben p2) //两点间距离。。。

{

    return (p2.y - p1.y) * (p2.y - p1.y) + (p2.x - p1.x) * (p2.x - p1.x);
}

bool cmp(ben lhs, ben rhs)
{

    if (check(p[1], lhs, p[1], rhs) < 0)
        return false;

    if (check(p[1], lhs, p[1], rhs) > 0)
        return true;

    return d(p[1], lhs) < d(p[1], rhs);
}

void add(double ll, double ff)

{

    double mid;

    p[num].x = ll, p[num].y = ff;

    if (p[num].y < p[1].y || (p[num].y == p[1].y && p[num].x < p[1].x))
    {

        swap(p[num], p[1]);
    }

    num++;

    return;
}

int main()

{

    scanf("%d", &n);

    double mid, ll, ff;

    for (int i = 1; i <= n; i++)

    {

        scanf("%lf%lf", &ll, &ff);

        add(ll, ff);
    }

    sort(p + 2, p + num, cmp); //系统快排

    s[1] = p[1]; //最低点一定在凸包里

    int cnt = 1;

    for (int i = 2; i <= num - 1; i++)

    {

        while (cnt > 1 && check(s[cnt - 1], s[cnt], s[cnt], p[i]) <= 0) //判断前面的会不会被踢走，如果被踢走那么出栈

            cnt--;

        cnt++;

        s[cnt] = p[i];
    }

    s[cnt + 1] = p[1]; //最后一个点回到凸包起点

    if (cnt == 1)

        return 0;

    if (cnt == 2)

    {

        cout << fixed << setprecision(0) << d(s[1], s[2]) << endl;

        return 0;
    }

    for (int u = 1; u <= cnt; ++u)

    {

        while (check(s[u], s[u + 1], s[u + 1], s[v]) <=

               check(s[u], s[u + 1], s[u + 1], s[v + 1]))

        {

            v = v == cnt ? 1 : v + 1;
        }

        ans = max(ans, max(d(s[u], s[v]), d(s[u + 1], s[v])));
    }

    printf("%.0lf\n", ans);

    // for (int i = 1; i <= cnt; i++)

    //   ans += d(s[i], s[i + 1]); //然后s里存好了凸包序列，只需要把两两距离累加就行

    return 0;
}

kmp

****推荐学习网址****：https://www.cnblogs.com/-citywall123/p/11688576.html；

****注意****：

*在有符号整型和无符号整型的比较中，自动将有符号整型数转换为无符号整型。*

C++方法：

不要尝试理解kmp算法，与递归同理

下面是求****Next****数组的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <iostream>

#include <string>

using namespace std;

const int n = 1008;

string s;

int Next[n];

void aa()

{

    Next[0] = -1;

    int i = 0;

    int j = -1;

    while (i <= s.length())

    {

        if (j == -1 || s[i] == s[j])

        {

            Next[++i] = ++j;
        }
        else

        {

            j = Next[j];
        }
    }
}

int main()

{

    cin >> s;

    aa();

    for (int i = 0; i < s.length(); i++)

    {

        cout << " " << Next[i] << " ";
    }

    return 0;
}

****下面是全的代码****：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
#include <iostream>

#include <cstring>

#include <string>

using namespace std;

const int n = 1e6 + 10;

int next1[n];

string re;

string te;

int re1, te1;

void get_ne()

{

    int i = 0;

    int j = -1;

    next1[0] = -1;

    //	**i在前面，j在后面**

    while (i < te1)

    {

        if (j == -1 || te[i] == te[j])

        {

            next1[++i] = ++j;
        }
        else
        {

            j = next1[j];
        }
    }
}

int get_piace()

{

    int i = 0;

    int j = 0;

    while (i < re1 && j < te1)

    {

        if (j == -1 || te[j] == re[i])

        {

            i++;

            j++;
        }

        else

        {

            j = next1[j];
        }
    }

    if (j >= te1)

    {

        return i - te1 + 1;
    }

    else
    {

        return -1;
    }
}

int main()

{

    cin >> re >> te;

    re1 = re.size();

    te1 = te.length();

    get_ne();

    cout << "查找到的位置初始是：" << get_piace() << endl //由一开始的

        return 0;
}

最长上升子序列 LIS

1.dp 最长联通串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include<bits/stdc++.h>
using namespace std;
int va[40][40];
int a[30];
int b[30];
int dp[30];
void dfs(int num)
{
	if(b[num]) dfs(b[num]);
	cout<<num<<" ";
}
int main()
{
    freopen("a.in","r",stdin);
    freopen("b.out","w",stdout);
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	
	for(int i=1;i<=n-1;i++)
	{
		for(int j=i+1;j<=n;j++)
		{
			int temp;
			cin>>temp;
			if(temp)
			{
				va[i][j]=1;
			}	
		}
	}
	int ans=0,pos=0;
	dp[1]=a[1];
	for(int i=2;i<=n;i++)
	{
		dp[i]=a[i];
		for(int j=i-1;j>=1;j--)
		{
			if(va[j][i]&&dp[i]<dp[j]+a[i])
			{
				dp[i]=dp[j]+a[i];
				b[i]=j;
			}
		}
		if(ans<dp[i])
		{
			ans=dp[i];
			pos=i;
		}
	}
	dfs(pos);
	cout<<endl<<ans;
	
	return 0;
}

2.二分实现时间更短

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;

const int maxn = 1e5 + 5;

int a[maxn], f[maxn];
int cnt;

inline int find(int x) {
    int l = 1, r = cnt; 
    while(l < r) {
        int mid = l + r >> 1;
        if(f[mid] >= x) r = mid;
        else l = mid + 1;
    }

    return l;
}

int main(void) {
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++) scanf("%d", &a[i]);

    f[++cnt] = a[1];
    for(int i = 2; i <= n; i ++) 
        if(a[i] > f[cnt]) f[ ++ cnt] = a[i];
        else {
            int tmp = find(a[i]);
            f[tmp] = a[i]; 
        }

    printf("%d\n", cnt);

    return 0;
}

LCS最长公共子序列

相当于用数组映射让第一个数组单调递增，之后数组映射获得在此情况下的另一个数组，最后要求的结果就变成了lis

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<bits/stdc++.h>
using namespace std;
const int N=1e6;
int a[N],b[N],f[N],mp[N];

int main()
{ 
	freopen("a.in","r",stdin);
    freopen("b.out","w",stdout);
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		mp[a[i]]=i;
	}
	for(int i=1;i<=n;i++)
	{
		cin>>b[i];
		f[i]=0x3f3f3f3f;
	}
	f[0]=0;
	int len=0;
	for(int i=1;i<=n;i++)
	{
		if(mp[b[i]]>f[len])
		{
			f[++len]=mp[b[i]];
		}else{
			*lower_bound(f,f+len,mp[b[i]])=mp[b[i]];
		}
	}
	cout<<len<<endl;

	return 0; 
}